
Equivalent Ratios
MA.6.AR.3.3 Extend previous understanding of fractions and numerical patterns to generate or complete a two- or three-column table to display equivalent part-to-part ratios and part-to-part-to-whole ratios.
Objectives: Students will be able to identify and create equivalent ratios using a table.
What is an Equivalent Ratio?
An equivalent ratio is a ratio that we get by either multiplying or dividing the two quantities being compared by the same number.
To get a ratio equivalent to a given ratio, we first represent the ratio in fraction form. Then, multiplying or dividing the first term and the second term by the same non-zero number, we can get the equivalent fraction. At last, we represent it in the ratio form.
Watch the following video explaining how to find equivalent ratios.
Now You Try It!
Example One:
Which of the following are equivalent ratios?
1. 1:2 and 2:4
2. 3:4 and 6:8
3. 3:4 and 9:8
3. 1:5 and 3:15
4. 12:3 and 4:3
5. 12:6 and 6:2
Answers:
1. These two ratios are equivalent ratios! If you write the ratios as fractions, then you will see that they are equal. If you simplify 2/4 you will get the first ratio, 1/2.
2. These two ratios are equivalent ratios! If you write the ratios as fractions, then you will see that they are equal. If you simplify 6/8 you will get the first ratio, 3/4.
3. These two ratios are not equivalent ratios! If you write the ratios as fractions, you will see that 9/8 cannot simplify any further. If you multiply the ratio 3/4 by 3, you will get 9/12, not 9/8.
4. These two ratios are not equivalent ratios! If you write the ratios as fractions, you will see that 12/3 simplifies to 4/1, not 4/3.
5. These two ratios are not equivalent ratios! If you write the ratios as fractions, you will see that 12/6 simplifies to 6/1, not 6/2.
Example Two:
Watch the following video on ratio tables. Then proceed to the problem for example two.
Problem: A store you're shopping at is having a back-to-school sale. You can get three free pencils for every two notebooks that you buy. How many pencils will you get if you buy 4 notebooks? 6 notebooks? 8 notebooks?
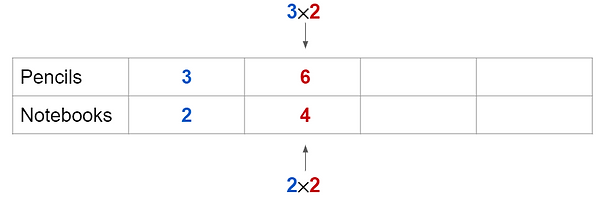
Step 1) Create a table! Make sure that 3:2 is the first ratio in your table.
Step 2) The question first asks how many pencils you would get if you bought 4 notebooks. How many times did you multiply the number of notebooks (2) to get 4? You multiplied 2 by 4. Now, write 4 in the next box for notebooks. Remember, anything you do to one quantity you must do to the other! Multiply the number of pencils (3) by the same number! 3 times 2 gives you 6. Write your answer in the table.
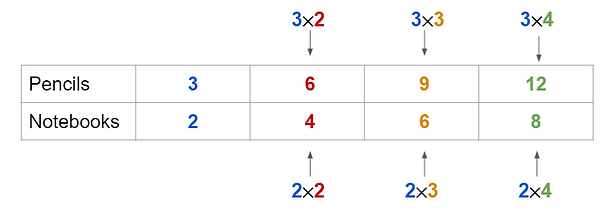
Step 3) The question then asks how many pencils you will get if you buy 6 notebooks. How do you get from 2 notebooks to 6 notebooks? You can multiply the number of notebooks (2) by 3! Next, multiply the number of pencils by the same number!
Step 4) Lastly, the question asks how many pencils you will get if you buy 8 notebooks. How do you go from 2 notebooks to 8 notebooks? Well, we can multiply 2 by 4 to get 8. Write the new number of notebooks in the table. Then, multiply the original number of pencils by the same number (4) to get the new ratio of pencils to notebooks.
Answer: If you buy 4 notebooks, you will get 6 pencils.
If you buy 6 notebooks, you will get 9 pencils.
If you buy 8 notebooks, you will get 12 pencils.
Notice: Did you notice a pattern? The number of pencils is increasing by 3 each time and the number of notebooks is increasing by 2 each time! Remember, 3:2 was our original ratio!
Take a Look!
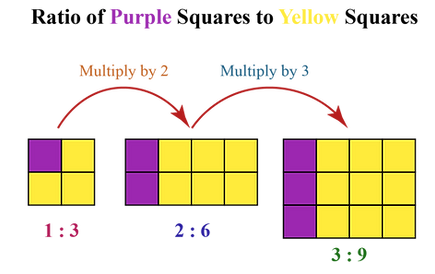
Look at the following examples of equivalent ratios. Take notice of how ratios can be represented visually and mathematically.


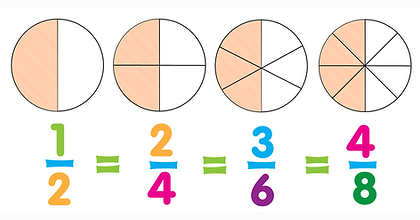
Click the link to play a fun game involving equivalent ratios!