
Percent Proportions
MA.6.AR.3.4 Apply ratio relationships to solve mathematical and real-world problems involving percentages using the relationship between two quantities.
Objectives: Students will be able to find a missing part or a whole and a missing percent given a scenario.
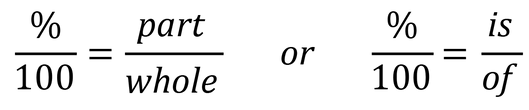
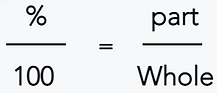

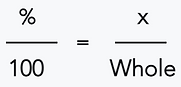
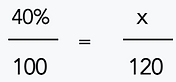
Introduction to Percents
A percent is a number or ratio expressed as a fraction of 100. It is often denoted using the percent sign "%".
For example, if you took a test and got 80 out of 100 questions right, you would have scored an 80%. You can also right this as a ratio: 80:100, meaning there are 80 correct answers for every 100 questions!
Watch the following video that gives you a greater look into percents.
Example One:
Answer the following scenarios.
1. You went to the store and bought a pair of $100.00 jeans for 50% off. How much did you buy the jeans for?
2. You took a test and got 10 questions correct out of 100. What was your score? Write your answer as a percent.
Answers:
1. $50. Remember, "per cent" means "per 100". If you got 50 percent off, you got 50 "per hundred" off. So, what is 100-50? 50! Another way to think about this is 50% actually means "half"! So, if your $100 jeans were half off, you would divide 100 by 2 and you would get 50.
2. 10%. If you answered 10 questions correctly out of 100, you would have the ratio 10:100 or 10/100.
Setting up a Percent Proportion.
A percent proportion is an equation in which a ratio is set equal to a percent ratio. The percent proportion can help you find a missing part, whole, or determine a percent given a scenario.
This is an example of how a part-to-whole percent proportion would be set up:
Notice that you can write a percent proportion in two different ways but they mean the same thing. When given a word problem, you can use key words like "is" and "of" to figure out what is your "part" and what is your "whole".
If you are given a question that asks you, "what percent of 18 is 9?" Your part would be 9 and your whole would be 18.
Watch the following video about percent proportions. Pause the video and attempt to answer the questions on your own if you can!
Example Two:
What percent of $15 is $9?
Step 1) Determine if you are finding the part, the whole, or the percent.
Because the question asks "what percent...", we know we are trying to find the percent.
Step 2) We know that $15 is our whole because of the word "of" before $15.
We know that $9 is our part because of the word "is" before $9.
Step 3) Cross multiply.
900 = 15x
Step 4) Divide. You want to isolate the x, so make sure to divide the coefficient, or the number infront of the x, from both sides.
60 = x
Step 5) Remember, you cannot leave your answer as 60! The question asked for a percent. Add the "%" to finalize your answer.
Note: 60 and 60% have very different values! Do not forget to add the "%" or your answer will be incorrect.
Answer: 60%
Example Three:
What number is 40% of 120?
Step 1) Determine whether you are finding the part, the whole, or the percent.
Since we are given the percent (40%), we know we are looking for a part or a whole.
Since the word "of" is in front of 120, we know that 120 is our whole.
Therefore, we are looking for a part ("is").
Step 2) Set up the percent proportion.
Step 3) Cross multiply.
4,800 = 100x
Step 4) Divide. You want to isolate the x, so divide both sides by 100.
48 = x
Answer: 40% of 120 is 48.