
Proporciones porcentuales
MA.6.AR.3.4 Aplicar relaciones de razón para resolver problemas matemáticos y del mundo real que involucran porcentajes usando la relación entre dos cantidades.
Objetivos: Los estudiantes podrán encontrar una parte o un todo faltante y un porcentaje faltante dado un escenario.
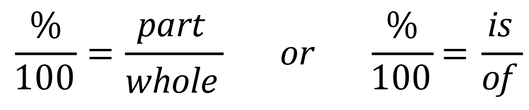
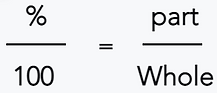

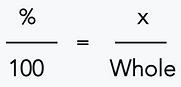
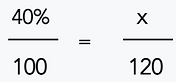
Introducción a los porcentajes
A por ciento es un número o razón expresada como una fracción de 100. A menudo se denota con el signo de porcentaje "%".
Por ejemplo, si hiciste un examen y acertaste 80 de 100 preguntas, habrías obtenido un 80% . También puede corregir esto como una proporción: 80: 100 , lo que significa que hay 80 respuestas correctas por cada 100 preguntas .
Mire el siguiente video que le brinda una mayor visión de los porcentajes.
Ejemplo uno:
Responda los siguientes escenarios.
1. Fuiste a la tienda y compraste un par de jeans de $ 100.00 con un 50% de descuento. ¿Por cuánto compraste los jeans?
2. Hiciste un examen y obtuviste 10 preguntas correctas de 100. ¿Cuál fue tu puntaje? Escribe tu respuesta como porcentaje.
Respuestas:
1. $ 50. Recuerde, "por ciento" significa "por 100". Si tiene un 50 por ciento de descuento, obtiene un 50 por ciento de descuento. Entonces, ¿qué es 100-50? 50! ¡Otra forma de pensar en esto es que el 50% en realidad significa "la mitad"! Entonces, si sus jeans de $ 100 fueran la mitad de descuento, dividiría 100 entre 2 y obtendría 50.
2. 10%. Si respondió correctamente 10 preguntas de 100, tendría una proporción de 10: 100 o 10/100.
Configuración de una proporción porcentual.
Una proporción porcentual es una ecuación en la que una proporción se establece igual a una proporción porcentual. La proporción porcentual puede ayudarlo a encontrar una parte faltante, un todo o determinar un porcentaje dado un escenario.
Este es un ejemplo de cómo se configuraría una proporción de porcentaje de parte a todo:
Observe que puede escribir una proporción porcentual de dos formas diferentes, pero significan lo mismo. Cuando se le presente un problema verbal, puede usar palabras clave como "es" y "de" para averiguar cuál es su "parte" y cuál es su "todo".
Si le dan una pregunta que le pregunte, " ¿qué porcentaje de 18 es 9? " Su parte sería 9 y su total sería 18 .
Mire el siguiente video sobre proporciones porcentuales. ¡Pausa el video e intenta responder las preguntas por tu cuenta si puedes!
Ejemplo dos:
¿Qué porcentaje de $ 15 es $ 9?
Paso 1) Determine si está encontrando la parte, el todo o el porcentaje.
Debido a que la pregunta pregunta " qué porcentaje ... ", sabemos que estamos tratando de encontrar el porcentaje.
Paso 2) Sabemos que $ 15 es nuestro total debido a la palabra " de " antes de $ 15.
Sabemos que $ 9 es nuestra parte porque la palabra " es " antes de $ 9.
Paso 3) Multiplicar en cruz.
900 = 15 veces
Paso 4) Dividir. Quieres aislar la x, así que asegúrate de dividir el coeficiente, o el número enfrente de la x, de ambos lados.
60 = x
Paso 5) Recuerde, ¡no puede dejar su respuesta como 60! La pregunta pedía un porcentaje. Agrega el "%" para finalizar tu respuesta.
Nota: ¡ 60 y 60% tienen valores muy diferentes! No olvide agregar el "%" o su respuesta será incorrecta.
Respuesta: 60%
Ejemplo tres:
¿Qué número es el 40% de 120?
Paso 1) Determina si estás encontrando la parte, el todo o el porcentaje.
Dado que se nos da el porcentaje (40%), sabemos que estamos buscando una parte o un todo.
Dado que la palabra "de" está delante de 120, sabemos que 120 es nuestro todo.
Por lo tanto, buscamos una parte ("es").
Paso 2) Configure la proporción porcentual.
Paso 3) Multiplicar en cruz.
4.800 = 100x
Paso 4) Dividir. Quieres aislar la x, así que divide ambos lados por 100.
48 = x
Respuesta: 40% de 120 es 48.